Elevation Grade
What is Elevation Grade?
Grade of an object’s physical feature, a landform or a line (plane) is used to indicate the slope of the thing being measured. Applications of grade include physical features like hills, riverbanks and canyons and construction aspects such as roads, roof pitch and landscaping. In other words, how to find elevation grade is an important skill in many areas.
Grade is also commonly called incline or rise. Depending on the method used to finding elevation grade, it can be expressed in different ways like decimal, percentage and degree.
How to Calculate Elevation Grade
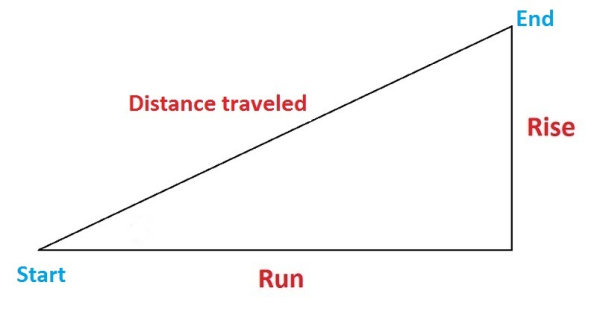
Before you figure out elevation grade, elevations must be taken from the starting and ending points for comparison, as well as the starting and ending distances. Keep in mind the distance traveled is not the same as the “run” (covered in the next section). 'Distance traveled' is the distance traversed between the starting and ending points, not necessarily the 'run' distance.
Be sure all your units are the same throughout.
As a Decimal
An easy-to-remember equation for finding change in elevation as a decimal is “rise over run,” meaning the rise (the change in vertical distance) divided by the run (the change in horizontal distance). As an example, let’s say the rise is 2 and the run is 6. So, you’d take 2 over 6 (or 2/6) to get .33 – that’s your grade as a decimal.
As a Percentage
The process for measuring elevation as a percentage is the same as finding elevation change as a decimal, with one extra step. So, find the rise over run. In our example, it’s 2 over 6 (2/6) – this is .33. Then simply multiply the decimal by 100 to find the percentage. In this case, 33%. A positive percentage indicates an upward slope. A positive number indicates an upward slope, and vice versa.
In Degrees
In trigonometric terms, grade is the tangent of the angle of a surface being measured to the horizontal. The larger the number, the greater the grade (or ‘tilt’). In this case, grade is expressed in degrees. For example, the elevation grade of a street could be 6.2°, meaning the street tilts upward 6.2° from horizontal (the horizon). In other words, you’re traveling uphill.
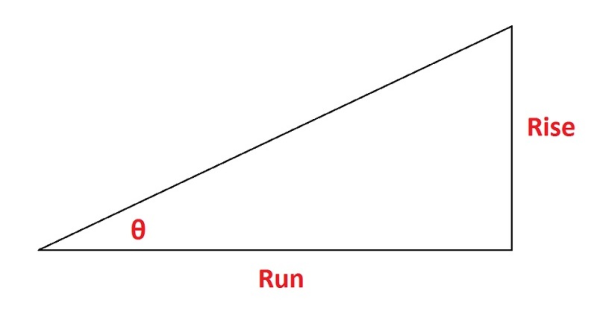
When calculating elevation slope in degrees, it’s helpful to think of the problem as a right triangle. Using basic trigonometry, you can find grade in degrees quickly. The diagram below shows the three basic aspects you’ll need to find grade.
Simply take “rise over run” and use arctangent (tan-1) to find theta (θ) – that’s your grade in degrees. Returning to our example, the rise is 2 and the run is 6. So, you’d take 2 over 6 (or 2/6) to get .33. Take the arctangent of .33, which is 18.26. Therefore, your grade is 18.26°. A positive number indicates an upward slope, and vice versa.
Practical Application of Calculating and Finding Elevation Grade
The rise over run equation can be applied to set simple grading for patios, walkways or driveways. Every project is different and there is no single way to set grade stakes for each and every job site.
Here is a walkthrough for grading of a simple slope in one direction using grade stakes. You may mark either stake as "cut" or "fill" depending on the landscape. In this example, we'll be describing a scenario in which you will be cutting grade.
How to Set Grade Stakes
- Pound grade stakes into the ground on each end of the area you need sloped. The stake at the top of the slope is called the hinge. The stake at the bottom of the slope is called the toe.
- Determine the desired grade—typically 1-2% (1/8" per foot to 1/4" per foot) is enough to provide enough runoff.
- Tie a string at a fixed height on the hinge.
- Run the string across the site and tie it on the toe tautly at the same fixed height on the stake.
- Place a line level on the taut string. Move the string from the toe end to make the string level.
- Mark where the level string ties to the stake. Let's say for this example you moved the string up 0.5" (meaning the current drop is 0.5").
- Assume the length between the stakes is 6 feet and you want a 2% grade. 1/4" x 6 = 1.5 inches. This means you want to toe to be 1.5 inches below the hinge.
- The difference between the desired grade (1.5") and the current grade (0.5") is how much you must cut from the toe stake.
- In this case, you must dig down 1" from the bottom of the current grade to reach the desired 2% grade.
How to Use a Transit for Elevations
Every angle is comprised the result of a set of 3 points being compared. Transit levels can be used to help you figure out the angle created by a set of three objects, and the distance between each object relative to the other two. Once you know these measurements, you can plug the numbers into the above equations, and figure out the slope.
For more information or help, refer to Johnson Level's collection of how-to guides.



































